Muốn tính được thể tích khối lăng trụ thì bạn cần nhớ chính xác mỗi công thức và vận dụng nó một cách linh hoạt vào giải toán. Cụ thể nó gồm những công thức nào? Vận dụng sao cho hiệu quả? Hãy xem chi tiết bài viết dưới đây.
1. Hình lăng trụ là gì?
Hình đa diện có mặt đáy là hai đa giác bằng nhau và mặt bên là các hình bình hành thì gọi là hình lăng trụ
Dựa vào mặt đáy hoặc sự tương quan giữa cạnh bên và mặt đáy mà hinh lăng trụ có các tên gọi khác nhau
- Nếu mặt đáy là tam giác thì tên gọi: khối lăng trụ tam giác
- Nếu mặt đáy là tam giác đều thì tên gọi: Khối lăng trụ tam giác đều
- Nếu mặt đáy là tứ giác thì tên gọi: Khối lăng trụ tứ giác
- Nếu các mặt bên vuông góc với mặt đáy: Khối lăng trụ đứng và trường hợp không vuông góc gọi là khối lăng trụ xiên
- Nếu mặt đáy là hình chữ nhật, lại vuông góc với mặt bên: Hình hộp chữ nhật
- Nếu lăng trụ tứ giác có các cặp cạnh đôi một vuông góc với nha và độ dài các cạnh bằng nhau thì ta gọi là hình lập phương
2. Công thức tính thể tích khối lăng trụ
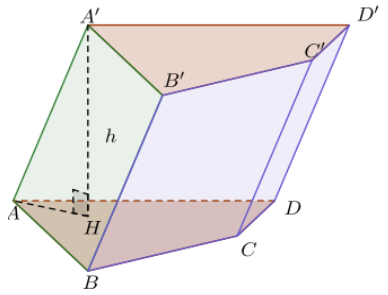
Công thức: V = S.h
- S là diện tích đáy
- h là chiều cao lăng trụ
Dựa theo mặt đáy của hình lăng trụ mà ta có các tên gọi khác nhau
2.1 Hình lăng trụ xiên
Lăng trụ tam giác
Là hình lăng trụ có mặt đáy là tam giác
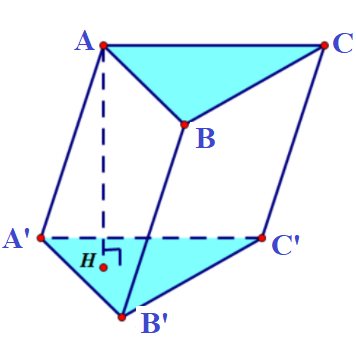Thể tích hình lăng trụ tam giác V = AH.SΔABC = AH.SΔA’B’C’
Tỉ số thể tích của lăng trụ đáy là tam giác
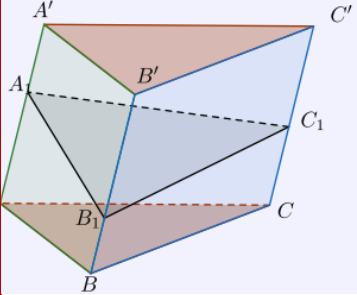
Công thức: $\left. \begin{array}{l} a = \frac{{{A_1}A’}}{{AA’}}\\ b = \frac{{{B_1}B’}}{{BB’}}\\ c = \frac{{{C_1}C’}}{{CC’}} \end{array} \right\} \to \frac{{{V_{A’B’C’.{A_1}{B_1}{C_1}}}}}{{{V_{ABC.A’B’C’}}}} = \frac{{a + b + c}}{3}$
Lăng trụ hình tứ giác
Là hình lăng trụ có mặt đáy là tứ giác
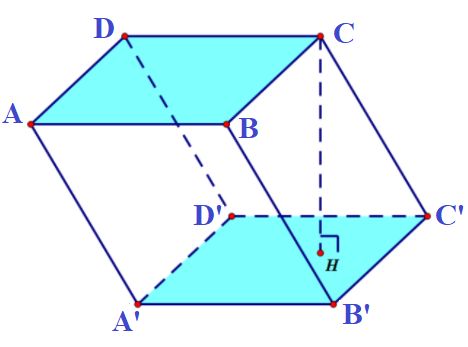
Thể tích hình lăng trụ tứ giác V = CH.SABCD = CH.SA’B’C’D’
Tỉ số thể tích của lăng trụ đáy là tứ giác
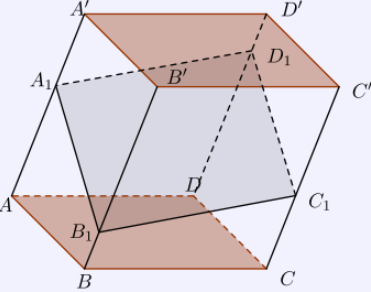
Công thức: $\left. \begin{array}{l} a = \frac{{{A_1}A’}}{{AA’}}\\ b = \frac{{{B_1}B’}}{{BB’}}\\ c = \frac{{{C_1}C’}}{{CC’}}\\ d = \frac{{{D_1}D’}}{{{\rm{DD}}’}} \end{array} \right\} \to \frac{{{V_{A’B’C’D’.{A_1}{B_1}{C_1}{D_1}}}}}{{{V_{ABCD.A’B’C’D’}}}} = \frac{{a + c}}{2} = \frac{{b + d}}{2}$
2.2 Hình lăng trụ đứng
Đây là hình lăng trụ có các cạnh bên vuông góc với mặt đáy
Lăng trụ đứng tam giác
Là hình lăng trụ tam giác có các cạnh bên vuông góc với mặt đáy.
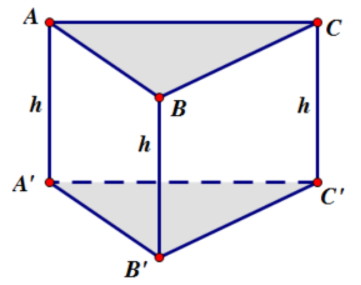
Thể tích lăng trụ đứng tam giác: V = h.SΔABC = h.SΔA’B’C’ trong đó h = AA’ = BB’ = CC’
Lưu ý: Nếu lăng trụ có đáy tam giác đều thì người ta có tên gọi khác là lăng trụ tam giác đều.
Lăng trụ đứng tứ giác
Là lăng trụ tứ giác có các cạnh bên vuông góc với mặt đáy.
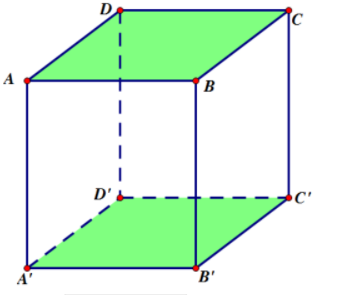
Thể tích lăng trụ đứng tứ giác: V = h.SABCD = h.SA’B’C’D’ trong đó h = AA’ = BB’ = CC’ = DD’
Ví dụ: Một lăng trụ đứng có đáy là tứ giác diện tích Sđáy = 2 cm2 và chiều cao 3 cm. Hãy tìm thể tích của lăng trụ đứng này
Lời giải
Theo đề:
- Sđáy = 2 cm2
- h = 3 cm
nên thể tích cần tìm: V = h.Sđáy = 2.3 = 6 cm3.
2.3 Hình hộp
Hình lăng trụ có đáy là hình chữ nhật gọi là hình hộp
Nếu hình lăng trụ đứng có đáy là hình chữ nhật thì tên gọi thường dùng: hình hộp chữ nhật
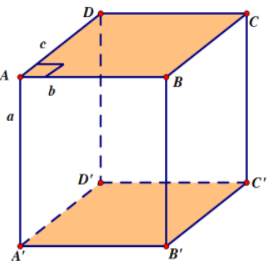
Gọi a, b, c lần lượt là các cạnh của hình hộp chữ nhật được biểu diễn như hình vẽ ở trên.
Khi đó công thức tính thể tích hình hộp chữ nhật là V = a.b.c
Ví dụ: Một hình hộp chữ nhật có chiều cao 5 cm; đáy là hình chữ nhật có chiều dài 3 cm và chiều rộng 2 cm. Hãy tìm thể tích của hình hộp chữ nhật này
Lời giải
Theo đề: $\left\{ \begin{array}{l} a = 5\left( {cm} \right)\\ b = 3\left( {cm} \right)\\ c = 2\left( {cm} \right) \end{array} \right. \Rightarrow V = a.b.c = 5.3.2 = 30\left( {c{m^3}} \right)$
Nếu hình hộp chữ nhật có tất cả các cạnh bằng nhau thì tên thường gọi: Hình lập phương
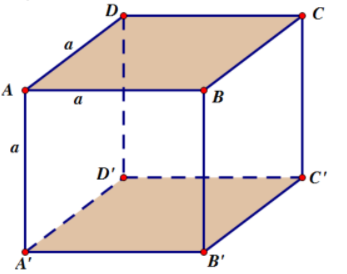
Công thức tính thể tích hình lập phương: V = a3 với a độ dài của cạnh hình lập phương.
Ví dụ: Cho hình lập phương ABCD.A’B’C’D’ có cạnh dài là 1 cm. Hãy tính thể tích khối lập phương này.
Lời giải
Vì cạnh dài a = 1 cm nên thể tích của khối lập phương này là V = a3 = 13 = 1 (cm3)
3. Bài tập
Bài 1: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$ có đáy $ABC$ là tam giác vuông tại $A$, $AC=a$, $\widehat{ACB}=60{}^\circ $. Đường thẳng $B{C}’$ tạo với $\left( AC{C}'{A}’ \right)$ một góc $30{}^\circ $. Tính thể tích $V$ của khối trụ $ABC.{A}'{B}'{C}’$.
A. $V={{a}^{3}}\sqrt{6}$.
B. $V=\frac{{{a}^{3}}\sqrt{3}}{3}$.
C. $V=3{{a}^{3}}$.
D. $V={{a}^{3}}\sqrt{3}$.
Lời giải
Chọn A.
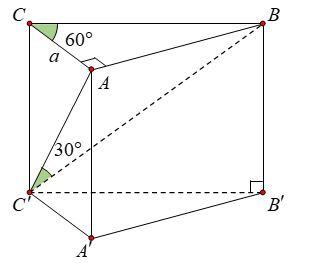
Vì tam giác ΔABC có góc A vuông nên
$\tan {{60}^{o}}=\frac{AB}{AC}\Rightarrow AB=a\sqrt{3}$.
Khi đó hình chiếu vuông góc của cạnh $B{C}’$ trên mặt phẳng $\left( AC{C}'{A}’ \right)$ là $A{C}’$.
Nên góc $\widehat{B{C}’A}=30{}^\circ $
Xét tam giác $AB{C}’$ vuông tại $A$ ta có: $\tan 30{}^\circ =\frac{AB}{A{C}’}\Rightarrow A{C}’=3a$ .
Khi đó: $C{C}’=\sqrt{A{{{{C}’}}^{2}}-A{{C}^{2}}}=2a\sqrt{2}$ .
Vậy ${{V}_{ABC.{A}'{B}'{C}’}}=C{C}’.{{S}_{\Delta ABC}}={{a}^{3}}\sqrt{6}$.
Bài 2: Khối hộp chữ nhật $ABCD.A’B’C’D’$ có $AB=a$, diện tích của $ABCD$ và $ABC’D’$ lần lượt bằng $2{{a}^{2}}$ và ${{a}^{2}}\sqrt{5}$. Thể tích khối chữ nhật bằng
A. $2{{a}^{3}}$.
B. ${{a}^{3}}\sqrt{5}$.
C. $3{{a}^{3}}$.
D. $\frac{\sqrt{5}{{a}^{3}}}{2}$.
Lời giải
Chọn A.
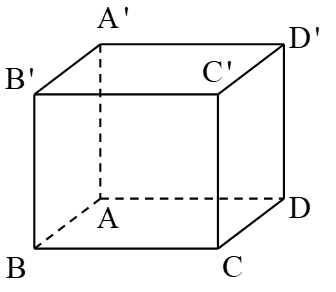
Diện tích $ABCD$ bằng $2{{a}^{2}}$ nên $BC=2a$. Diện tích của $ABC’D’$ bằng ${{a}^{2}}\sqrt{5}$ nên $BC’=a\sqrt{5}$.
$CC’=\sqrt{BC{{‘}^{2}}-B{{C}^{2}}}=a$. Vậy thể tích khối chữ nhật bằng
$AB.BC.CC’=2{{a}^{3}}.$
Chọn đáp án A.
Bài 3. Một lăng trụ ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Biết thể tích của hình lăng trụ này bằng $3{{a}^{3}}$. Hỏi chiều của của hình lăng trụ ABCD.A’B’C’D’ bằng bao nhiêu?
A. h = a.
B. h = 3a.
C. h = 9a.
D. $h=\frac{a}{3}$.
Lời giải
Chọn B.
Vì là hình vuông nên đáy có diện tích ${{S}_{ABCD}}={{a}^{2}}$.
Từ công thức thể tích khối lăng trụ hình hộp ta có: $h=\frac{{{V}_{ABCD.{A}'{B}'{C}'{D}’}}}{{{S}_{ABCD}}}=\frac{3{{a}^{3}}}{{{a}^{2}}}=3a$.
Trên đầy là toàn bộ bài viết giúp bạn hiểu hình lăng trụ gì và các công thức tính thể tích khối lăng trụ. Hy vọng bài viết này đã giúp ích được bạn trong quá trình học tốt toán hình.
