Có thể bạn biết khá nhiều vật có hình trụ nhưng chưa biết công thức tính thể tích hình trụ tròn xoay và ứng dụng của công thức này trong cuộc sống. Nếu vậy, hãy theo dõi bài viết dưới đây để nhớ chính xác công thức cũng như cách vận dụng nó sao cho linh hoạt vào giải bài tập.
1. Thể tích hình trụ tròn xoay
Thể tích của hình trụ (hay gọi là khối trụ) được xác định theo công thức: V = πr2h
Một số công thức nhanh
Trường hợp 1: Thể tích khối tứ diện có 2 cạnh là đường kính 2 đáy
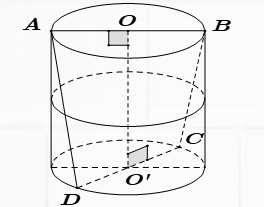
Đặc biệt: Nếu AB và CD vuông góc nhau thì: ${{V}_{ABCD}}=\frac{1}{6}AB.CD.OO’$
Trường hợp 2: Mối liên hệ giữa Sxung quanh, Stoàn phần và V của hình trụ tròn xoay.
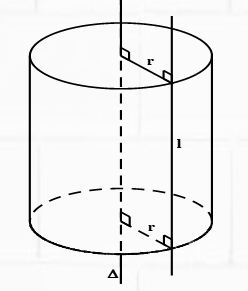
- Bài toán 1: Diện tích toàn phần nhỏ nhất: ${S_{tp}}\left( {\min } \right) \Leftrightarrow \left\{ \begin{array}{l} R = \sqrt[3]{{\frac{V}{{4\pi }}}}\\ h = 2\sqrt[3]{{\frac{V}{{4\pi }}}} \end{array} \right.$
- Bài toán 2: Smin = Sxung quanh + S1đáy: $S\left( {\min } \right) \Leftrightarrow \left\{ \begin{array}{l} R = \sqrt[3]{{\frac{V}{\pi }}}\\ h = \sqrt[3]{{\frac{V}{\pi }}} \end{array} \right.$
Trường hợp 3: Nếu hình trụ ngoại tiếp, nội tiếp một hình lăng trụ đứng thì thể tích khối lăng trụ là $V=\frac{4\pi V}{9}$
2. Bài tập
Bài 1: Một hình chữ nhật DABC có chiều rộng AB = 3 và chiều dài BC =4. Khi cho hình chữ nhật này quay quanh
- cạnh AB sinh ra hình trụ có thể tích V1
- cạnh BC sinh ra hình trụ có thể tích V2
Tìm tỉ số của V1/V2.
A. $\frac{11}{6}$
B. 2
C. 3/7
D. $\frac{4}{3}$
Đáp án là D
Bài 2: Một hình trụ tròn ngoại tiếp hình nón được biểu diễn như hình vẽ. Biết O, O’ là tâm hai mặt đáy hình trụ, OO′ = $r\sqrt 3 $. Gọi V1 là thể tích phần bên ngoài khối nón, V2 là phần thể tích bên trong khối nón. Khi đó $\frac{{{V}_{1}}}{{{V}_{2}}}$ bằng:
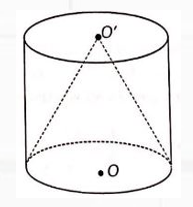
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. 2
D. 3
${{V}_{tru}}=B.h\Rightarrow \frac{{{V}_{1}}}{V}=\frac{1}{3}$
mặt khác $V={{V}_{1}}+{{V}_{2}}\Rightarrow \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{1}{2}$
Chọn đáp án A.
Bài 3: Một khối trụ có bán kính là R và chiều cao là h = $R\sqrt 2 .$ Điểm A thuộc đường tròn tâm O và điểm B thuộc đường tròn tâm O’, sao cho OA ⊥ OB. Gọi V là thể tích khối trụ, hãy tìm tỉ số thể tích sau: VOO’AB : V
A. $\frac{12}{13\pi }$
B. $\frac{11}{7\pi }$
C. $\frac{2}{3\pi }$
D. $\frac{1}{6\pi }$
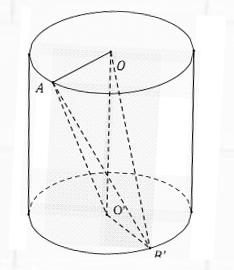
Lại có ${{S}_{OBO’}}=\frac{1}{2}O’O.O’B={{R}^{2}}\frac{\sqrt{2}}{2}\Rightarrow {{V}_{O.O’AB}}=\frac{\sqrt{2}}{6}{{R}^{3}}\Rightarrow $
$\frac{{{V}_{tru}}}{{{V}_{O.O’AB}}}=6\pi $.
Chọn D.
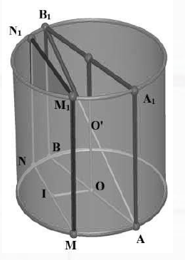
Bài 4: Cho một khối trụ như hình vẽ. Biết bán kính mặt đáy OA = r; Từ giác ACC’A’ là hình vuông. Giả sử V là thể tích hình trụ và V’ là thể tích lăng trụ đều nội tiếp. Hãy tìm tỉ số $\frac{V’}{V}$ là:
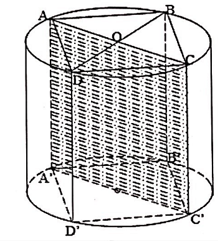
A. π
B. $\frac{\pi }{12}$
C. $\frac{2}{\pi }$
D. $\frac{10}{\pi }$
Do lăng trụ nội tiếp hình trụ có đáy là hình vuông nên cạnh dài bằng $r\sqrt{2}$.
Lúc này, thể tích lăng trụ nội tiếp là $V’={{\left( r\sqrt{2} \right)}^{2}}.2r=4{{r}^{3}}$
Tỉ số cần tìm $\frac{V’}{V}=\frac{4{{r}^{3}}}{2\pi {{r}^{3}}}=\frac{2}{\pi }$.
Chọn đáp án C.
Bài 5. Một lăng trụ tứ giác đều có mặt đáy cạnh dài là và mặt bên cạnh dài là 4a. Hỏi khối trụ nội tiếp trong hình lăng trụ có thể tích bằng bao nhiêu?
A. $\frac{\sqrt{2}}{8}$
B. $\frac{1}{3}$
C. $\frac{\sqrt{3}}{7}$
D. 2
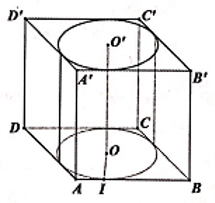
Trong khi đó chiều cao của hình trụ là h = 4a.
Thể tích khối trụ cần tìm là $V=\pi {{R}^{2}}h=\pi {{\left( \frac{a}{2} \right)}^{2}}.4a=\pi {{a}^{3}}$.
Chọn đáp án A.
Bài 6. Cho một hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hình này nội tiếp khối trụ. Hãy tính thể tích khối trụ này.
A. $V=\frac{\pi {{a}^{11}}}{4}$.
B. $V = 11\pi {a^3}$.
C. $V=\frac{\pi {{a}^{2}}}{7}$.
D. $V=\frac{\pi {{a}^{3}}}{2}$.
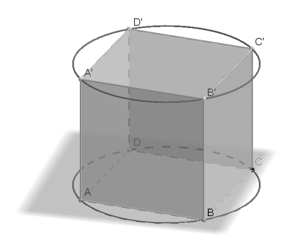
- chiều cao hình trụ là h = a
- Bán kính mặt đáy R = $AC\sqrt 2 $ = $\frac{{a\sqrt 2 }}{2}$
Ta biết hình lập phương nội tiếp khối trụ, thì thể tích khối trụ được xác định theo công thức $V=\frac{\sqrt{3}{{a}^{3}}}{3}$
=> $V=\pi {{R}^{2}}h=\pi .\frac{{{a}^{2}}}{2}.a=\frac{\pi {{a}^{3}}}{2}$.
Chọn đáp án D.
Bài 7. Cho một hình trụ tròn xoay như hình vẽ. Biết R = 1; AB = 2 và đường thẳng AB tạo với trụ khối trụ OO’ một góc 300. Xét hai khẳng định:
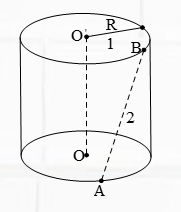
(II): Khối trụ có thể tích làà $V = \sqrt 3 \pi $
Kết luận nào sau đây là đúng?
A. Chỉ có nhận định (I) đúng.
B. Chỉ có nhận định (II) đúng.
C. Cả hai nhận định (I) và (II) đều sai.
D. Cả hai nhận định (I) và (II) đều đúng
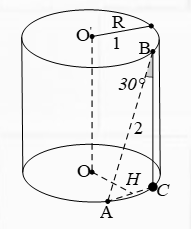
Vì (ABC) ⊥ (OAC) nên kẻ OH ⊥ AC ⇒ OH ⊥ (ABC).
Lúc này, khoảng cách d(OO’, AB) = OH
Tam giác ∆ABC có:
- BC = AB.cos300 = $\sqrt{3}$
- AC = AB.sin300 = 1
∆OAC có OA = OC = AC = 1 => OH =$\frac{\sqrt{3}}{2}$ : (I) đúng
Dựa vào công thức thể tích, ta có V = π.R2.h nên (II) đúng
Chọn đáp án D.
Bài 8. Một mặt cầu bán kính R ngoại tiếp hình trụ tròn xoay. Để thiết diện qua trục của hình trụ có Smax thì chiều cao của nó bằng bao nhiêu. Tính thể tích V và Stoàn phần của khối trụ này
A. $\frac{\pi {{R}^{3}}\sqrt{2}}{2};3\pi .{{R}^{2}}$
B. $\pi R;\frac{{\pi \sqrt 2 }}{2}.{R^2}$
C. $\pi {{R}^{3}}\sqrt{2};3\pi .{{R}^{2}}$
D. $\pi {R^2}\sqrt 6 ;\pi {R^2}$
Gọi h là chiều cao và r là bán kính mặt đáy thì diện tích thiết diện sẽ là ${{S}_{td}}=2r.h$ (1)
Mặt khác ${{R}^{2}}=O'{{A}^{2}}={{r}^{2}}+\frac{{{h}^{2}}}{4}\Rightarrow {{r}^{2}}={{R}^{2}}-\frac{{{h}^{2}}}{4}$
Từ biểu thức (1), ta có ${{S}_{td}}=h\sqrt{4{{R}^{2}}-{{h}^{2}}}=\sqrt{{{h}^{2}}\left( 4{{R}^{2}}-{{h}^{2}} \right)}$
đề Std = Smax khi h = R$\sqrt 2 $
Khi đó r = 0,5h, tức là thiết diện qua trục là hình vuông
$V=\pi {{r}^{2}}h=2\pi {{r}^{2}}.r=2\pi {{r}^{3}}=\frac{\pi {{R}^{3}}\sqrt{2}}{2};$
${S_{tp}} = 2\pi {r^3} + 2\pi rh = 3\pi {R^2}$
Chọn đáp án A.
Trên đây là toàn bộ bài viết về công thức tính thể tích hình trụ tròn xoay. Để học tốt bài này bạn cần xem bài diện tích xung quanh hình trụ tròn đã được chia sẻ từ bài trước. Hy vọng bài viết này hữu ích với bạn.