Nếu muốn học tốt chương 1 đại số lớp 12 thì điều đầu tiên bạn cần nhớ chính xác các công thức đạo hàm đã được học ở chương cuối đại số lớp 11. Tuy nhiên, một vài bạn vẫn quên hoặc nhớ không chính xác dẫn tới gặp những vướng mắc nhất định. Thấu hiểu được điều đó ToanC3 đã biên soạn chi tiết các công thức đạo hàm, những quy tắc đạo hàm, … chi tiết và đầy đủ nhất để bạn có thể ôn luyện từ đó bạn học nhanh, nhớ nhanh giúp việc giải các bài tập hay làm bài thi hiệu quả đạt kết quả cao.
Không chỉ hệ thống lại lý thuyết, công thức mà phần cuối có bài tập minh họa kèm lời giải nhằm khắc sâu kiến thức, rèn luyện kĩ năng giải bài đạo hàm tốt hơn.
Chúng ta bắt đầu vào bài viết hôm nay
1. Đạo hàm là gì?
Hàm số y = f(x) liên tục trên (a;b), được gọi là có đạo hàm tại x$_0$ ∈ (a;b) nếu giới hạn sau tồn tại (hữu hạn): $\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f(x)-f({{x}_{0}})}{x-{{x}_{0}}}$ và giá trị của giới hạn đó gọi là giá trị đạo hàm của hàm số tại điểm x$_0$.Ta kí hiệu f′(x$_0$).
Vậy $f'({{x}_{0}})=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f(x)-f({{x}_{0}})}{x-{{x}_{0}}}$
Tại điểm x$_0$, tỉ số giữa số gia của hs với số gia của đối số được gọi là Đạo Hàm.
Thông qua giá trị đạo hàm ta biết:
- Chiều biến thiên của hàm số
- Độ lớn của biến thiên
2. Quy tắc tính đạo hàm
Có 4 quy tắc cần nhớ là:
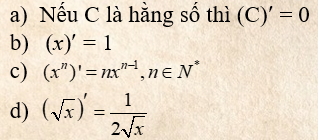
3. Đạo hàm của tổng, hiệu, tích, thương của hàm số
Khi gặp đạo hàm của một tổng-hiệu-tích hay thương thì bạn tuân theo:
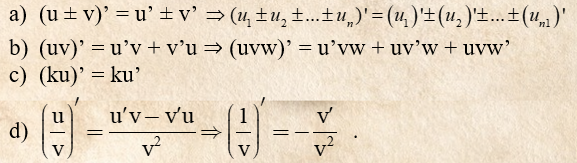
4. Đạo hàm của hàm số hợp
Giả sử y = G(u(x)) = G(u) với u = u(x). Khi đó $\left( {{y}_{x}} \right)’=\left( {{y}_{u}} \right)’.\left( {{u}_{x}} \right)’$
5. Bảng công thức đạo hàm các hàm cơ bản
5.1 Bảng đạo hàm cơ bản
Trường hợp: Đạo hàm của f(x) với x là một biến số
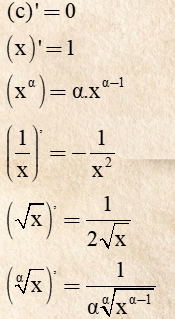
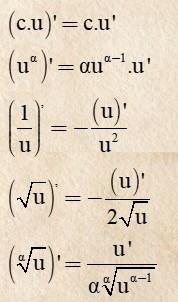
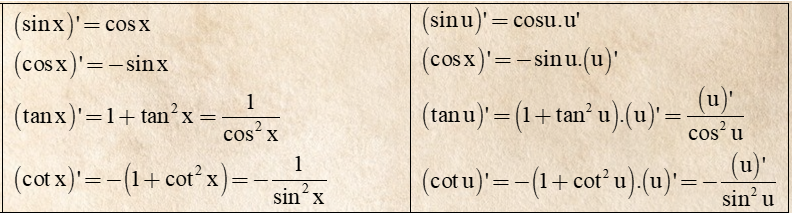
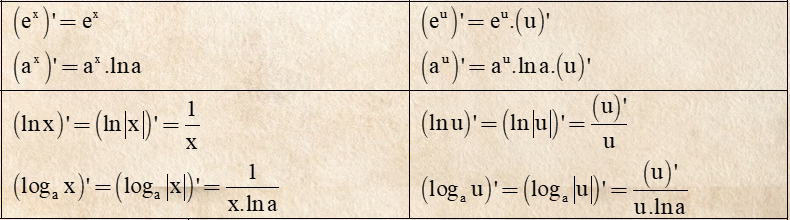
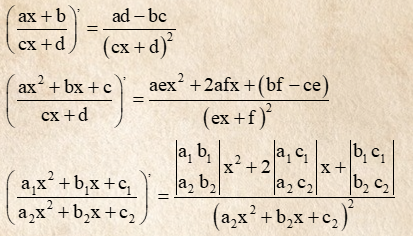
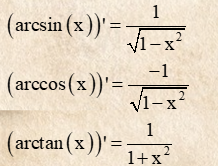
5.2 Bảng đạo hàm nâng cao
Đạo hàm lũy thừa
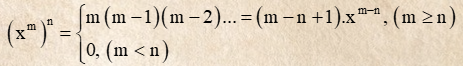
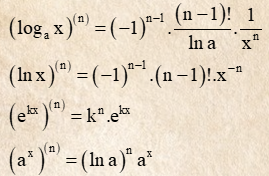
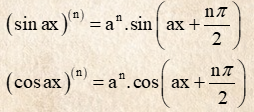
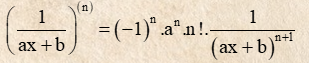
6. Bài tập đạo hàm
Bài tập 1. Tính đạo hàm các hàm số sau:
a) $y=-{{x}^{3}}+3x+1$
b) $y=\frac{{{x}^{2}}-2x+2}{x+1}$
Lời giải
a) Ta có: $y’={{\left( -{{x}^{3}}+3x+1 \right)}^{‘}}=-3{{x}^{2}}+3$
b) Ta có: $y’=\frac{({{x}^{2}}-2x+2)'(x+1)-({{x}^{2}}-2x+2)(x+1)’}{{{(x+1)}^{2}}}$
$=\frac{(2x-2)(x+1)-({{x}^{2}}-2x+2)}{{{(x+1)}^{2}}}=\frac{{{x}^{2}}+2x-4}{{{\left( x+1 \right)}^{2}}}$.
Bài tập 2. Giải bất phương trình $f'(x)\ge 0$ biết: $f(x)=\sqrt[4]{{{x}^{2}}+1}-\sqrt{x}$
Lời giải
TXĐ: $D=\left[ 0;+\infty \right)$
Ta có:$f'(x)=\frac{x}{2\sqrt[4]{{{({{x}^{2}}+1)}^{3}}}}-\frac{1}{2\sqrt{x}}$.
$f'(x)\ge 0\Leftrightarrow x\sqrt{x}\ge \sqrt[4]{{{({{x}^{2}}+1)}^{3}}}\Leftrightarrow {{x}^{6}}\ge {{({{x}^{2}}+1)}^{3}}$
$\Leftrightarrow {{x}^{2}}\ge {{x}^{2}}+1$ bất phương trình này vô nghiệm
Bài tập 3. Tính đạo hàm các hàm số sau:$y=\tan ({{\sin }^{2}}3x)+\sqrt{{{\cot }^{2}}(1-2{{x}^{3}})+3}$
Lời giải
Ta có: $y’=[1+{{\tan }^{2}}({{\sin }^{2}}3x)]({{\sin }^{2}}3x)’+\frac{[{{\cot }^{2}}(1-2{{x}^{3}})+3]’}{2\sqrt{{{\cot }^{2}}(1-2{{x}^{3}})+3}}$
$=3[1+{{\tan }^{2}}({{\sin }^{2}}3x)]\sin 6x+\frac{6{{x}^{2}}\text{ }\!\![\!\!\text{ }1+{{\cot }^{2}}(1-2{{x}^{3}})\text{ }\!\!]\!\!\text{ }\cot (1-2{{x}^{3}})}{\sqrt{{{\cot }^{2}}(1-2{{x}^{3}})+3}}$.
Bài tập 4. Tính đạo hàm của hàm số $y={{\left( \sqrt{x}-\frac{1}{\sqrt{x}} \right)}^{5}}$ .
Lời giải
Bước đầu tiên sử dụng ${{\left( {{u}^{\alpha }} \right)}^{/}}$với $u=\sqrt{x}-\frac{1}{\sqrt{x}}$
$y’ = 5{\left( {\sqrt x – \frac{1}{{\sqrt x }}} \right)^4}.{\left( {\sqrt x – \frac{1}{{\sqrt x }}} \right)^/}$$=5{{\left( \sqrt{x}-\frac{1}{\sqrt{x}} \right)}^{4}}.\left( \frac{1}{2\sqrt{x}}+\frac{{{\left( \sqrt{x} \right)}^{/}}}{{{\left( \sqrt{x} \right)}^{2}}} \right)$
$=5{{\left( \sqrt{x}-\frac{1}{\sqrt{x}} \right)}^{4}}\left( \frac{1}{2\sqrt{x}}+\frac{1}{2\sqrt{x}.x} \right)$
Bài tập 5. Tính đạo hàm cấp n của hàm số$y=\frac{2x+1}{{{x}^{2}}-5x+6}$
Lời giải
Ta có: $2x+1=7(x-2)-5(x-3)$; ${{x}^{2}}-5x+6=(x-2)(x-3)$
Suy ra $y=\frac{7}{x-3}-\frac{5}{x-2}$.
Mà ${{\left( \frac{1}{x-2} \right)}^{(n)}}=\frac{{{(-1)}^{n}}{{.1}^{n}}.n!}{{{(x-2)}^{n+1}}}=\frac{{{(-1)}^{n}}.n!}{{{(x-2)}^{n+1}}},$ ${\left( {\frac{1}{{x – 2}}} \right)^{(n)}} = \frac{{{{( – 1)}^n}.n!}}{{{{(x – 3)}^{n + 1}}}}$
Nên ${{y}^{(n)}}=\frac{{{(-1)}^{n}}.7.n!}{{{(x-2)}^{n+1}}}-\frac{{{(-1)}^{n}}.5.n!}{{{(x-3)}^{n+1}}}$.
Trên đây là những chia sẻ các công thức đạo hàm thường gặp khi giải bài tập cũng như làm bài thi. Nếu bạn thấy bài viết này hay hãy chia sẻ tới những người bạn khác để mọi người có được tài liệu toán học ôn tập hiệu quả. Chúc bạn học tập tốt.